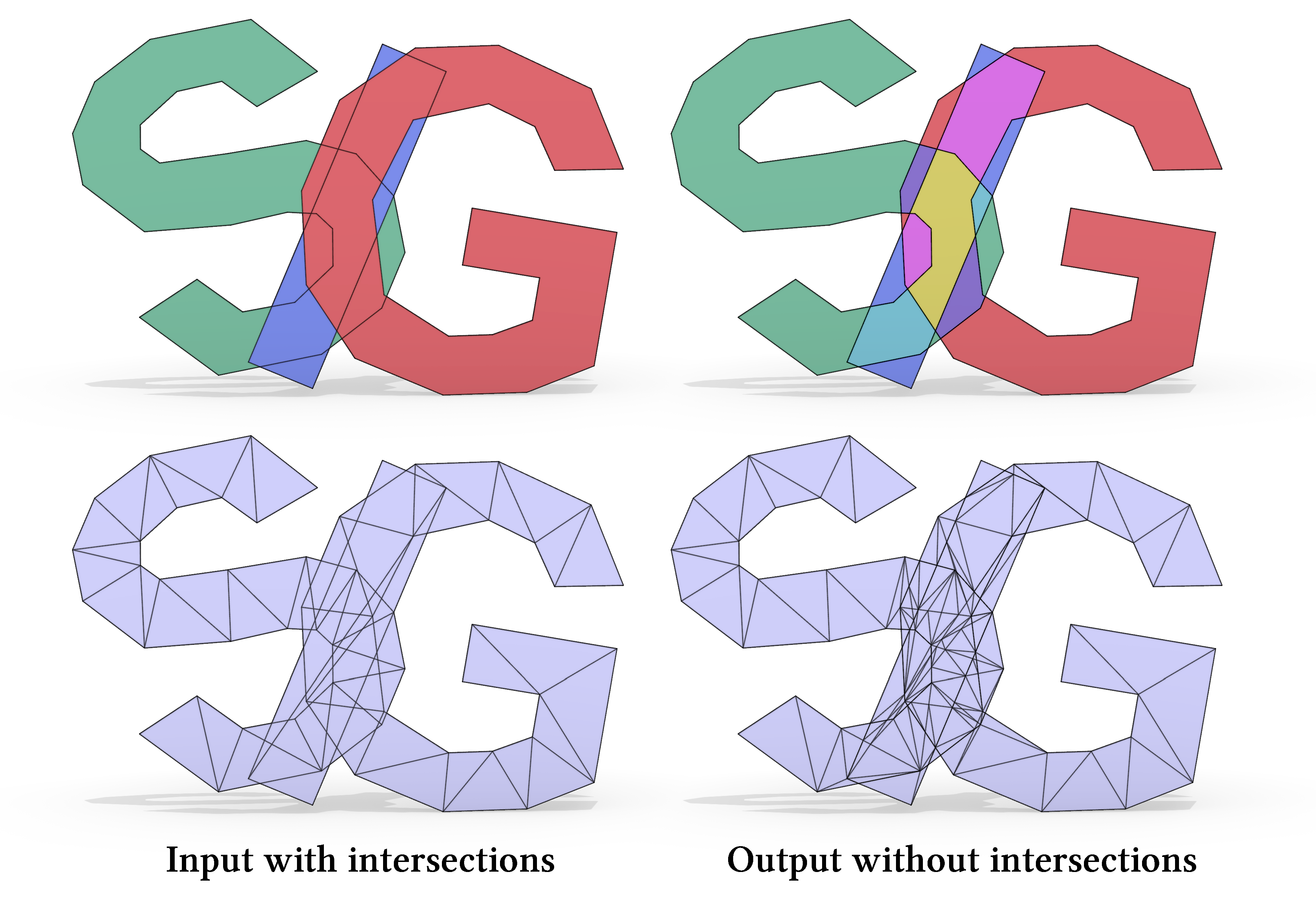
Exact and Efficient Intersection Resolution for Mesh Arrangements

Abstract

We propose a novel method to exactly and efficiently resolve intersections and self-intersections in triangle meshes. Our method contains two key components. First, we present a new concept of geometric predicates, called indirect offset predicates, to represent all intersection points through a new formulation and establish all necessary geometric predicates. Consequently, we reduce numerical errors in floating-point evaluations and improve the success rate of early stages of arithmetic filtering. Second, we develop localization and dimension reduction techniques for sorting, deduplicating, and locating the intersection points, thereby boosting efficiency and parallelism while maintaining accuracy. Rigorous testing confirms the robustness of our algorithm and consistency with previous methods. Comprehensive testing across diverse datasets further highlights the speed improvement achieved by our method, which is one order of magnitude faster than the state-of-the-art methods.

Results

We test our algorithm on the Thingi10k dataset and one stress-testing dataset (constructed by rotating one models several times and combining all of them) to validate the robustness and efficiency of our algorithm. Compared with the state-of-the-art methods, the efficiency is improved by an order of magnitude. See details in our paper :).

Resources

• Paper
• Supplementary
• Code
• Data

Acknowledgement

We would like to thank the anonymous reviewers for their constructive suggestions and comments. This work is partially supported by the National Natural Science Foundation of China (62272429).

Cite us

@article {guo2024arrangements,
    title = {Exact and Efficient Intersection Resolution for Mesh Arrangements},
    author = {Guo, Jia-Peng and Fu, Xiao-Ming}
    journal = {ACM Transactions on Graphics},
    volume={43},
    number={6},
    pages={1--14},
    year = {2024}
}